Planeta Ziemia
Czy Ziemia jest naprawdę okrągła?

Lycee J.Monet
Cognac, Francja
Zespół Szkół Handlowych
Sopot, Polska
Wszyscy wiemy, że Ziemia ma kształt kulisty, ale niełatwo jest to zobaczyć ze szkolnego podwórka. Przekonaj się sam że Ziemia jest okrągła i zmierz z nami jej promień korzystając z metody wynalezionej już w 240 r. p.n.e. przez Eratostenesa z Cyreny!
 |  | 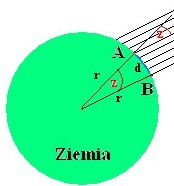 |
| Pomiar promienia Ziemi metodą Erastotenesa |
Program nauczania/Przedmioty:
Szkoła ponadgimnazjalna
Podstawa programowa: światło i jego rola w przyrodzie
temat: analiza spektralna
Szkoła ponadgimnazjalna
Podstawa programowa: światło i jego rola w przyrodzie
temat: analiza spektralna
Wstęp
Poglądy o kulistości Ziemi głosili już filozofowie szkoły pitagorejskiej, a Arystoteles w IV w. p.n.e. starał się zebrać dowody kulistości Ziemi:
· kolisty cień na Księżycu w czasie jego zaćmienia,
· stopniowe zmiany wysokości bieguna światła przy podróży wzdłuż południka,
· kołowy kształt widnokręgu,
· stopniowe wyłanianie się statków spoza horyzontu morskiego poczynając od wierzchołków masztów, gór – poczynając od szczytów.
Eratostenes założył, że Ziemia jest doskonałą kulą, i że odległość dwóch punktów znajdujących się na tym samym południku ma się tak do obwodu kuli ziemskiej, jak różnica między odpowiednimi wysokościami Słońca tego samego dnia w południe (różnica szerokości geograficznych tych punktów) do kąta pełnego (360º).
Około 240 r.pn.e. Eratostenes obliczył, że Słońce w Aleksandrii było odchylone od zenitu o 7º12' (7,2º), czyli z = 1/50 kąta pełnego. Aby zmierzyć obwód Ziemi, Eratostenes potrzebował jeszcze odległości między Aleksandrią a Syene. Oszacował ją na podstawie liczby dni, jakich potrzebowały karawany do pokonania tej odległości. Znając średnie tempo karawan, ustalił odległość na 5000 stadionów (stadiów) - nie ma pewności, ile liczył starożytny stadium, ale przyjmuje się, że 157,7 m - czyli około 800 km.
Uzyskany przez Erastostenesa wynik przypadkowo[1] różnił się stosunkowo niewiele od wartości rzeczywistej (46000 km zamiast 40000 km) wyznaczonej wiele wieków później metodami triangulacji.
[1] miasta nie znajdują się na tym samym południku (różnica długości geograficznej wynosi 3º), a i Słońce nie było w rzeczywistości 21 czerwca w Syene w zenicie.
· kolisty cień na Księżycu w czasie jego zaćmienia,
· stopniowe zmiany wysokości bieguna światła przy podróży wzdłuż południka,
· kołowy kształt widnokręgu,
· stopniowe wyłanianie się statków spoza horyzontu morskiego poczynając od wierzchołków masztów, gór – poczynając od szczytów.
Eratostenes z Cyreny, a pomiar obwodu Ziemi
 |
Grecki filozof żyjący w III w. p.n.e., zarządca Biblioteki Aleksandryjskiej, który jako pierwszy wyznaczył obwód Ziemi |
Eratostenes założył, że Ziemia jest doskonałą kulą, i że odległość dwóch punktów znajdujących się na tym samym południku ma się tak do obwodu kuli ziemskiej, jak różnica między odpowiednimi wysokościami Słońca tego samego dnia w południe (różnica szerokości geograficznych tych punktów) do kąta pełnego (360º).
Eratostenes jako punkty te przyjął:
· rodzinne miasto - Aleksandrię,
· Syene (obecny Assuan w Egipcie nad Nilem).
· Syene (obecny Assuan w Egipcie nad Nilem).
Jak podają źródła filozof dowiedział się (od kupców lub wyczytał w jednej z książek w Bibliotece Aleksandryjskiej), że Słońce w dniu przesilenia letniego - 21 czerwca, w południe - w Syene znajduje się w zenicie, ponieważ „promienie Słońca oświetlają dna najgłębszych studni, a wysokie słupy nie dają cienia”. W tym samym czasie w Aleksandrii słupy rzucały cień o pewnej długości.
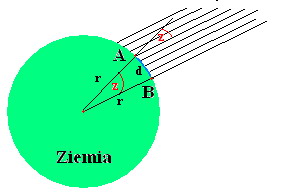 |
| A – Aleksandria, B – Syene (Assuan) d – odległość między Aleksandrią, a Syene, r – promień Ziemi z – kąt odchylenia promieni słonecznych od zenitu |
Około 240 r.pn.e. Eratostenes obliczył, że Słońce w Aleksandrii było odchylone od zenitu o 7º12' (7,2º), czyli z = 1/50 kąta pełnego. Aby zmierzyć obwód Ziemi, Eratostenes potrzebował jeszcze odległości między Aleksandrią a Syene. Oszacował ją na podstawie liczby dni, jakich potrzebowały karawany do pokonania tej odległości. Znając średnie tempo karawan, ustalił odległość na 5000 stadionów (stadiów) - nie ma pewności, ile liczył starożytny stadium, ale przyjmuje się, że 157,7 m - czyli około 800 km.
Uzyskany przez Erastostenesa wynik przypadkowo[1] różnił się stosunkowo niewiele od wartości rzeczywistej (46000 km zamiast 40000 km) wyznaczonej wiele wieków później metodami triangulacji.
[1] miasta nie znajdują się na tym samym południku (różnica długości geograficznej wynosi 3º), a i Słońce nie było w rzeczywistości 21 czerwca w Syene w zenicie.
Opis doświadczenia
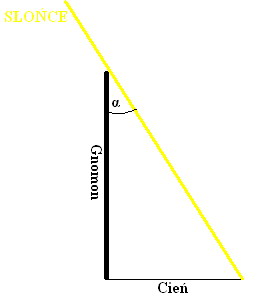
Zdecydowanie najtrudniejszą częścią doświadczenia jest znalezienie chętnego nauczyciela (szkoły) na tym samym południku i względnie odległego. Do przeprowadzenia doświadczenia potrzebne są gnomony (pionowe kije) i równe podłoże ( lub wypoziomowane tarcze z gnomonem). Kolejnym warunkiem przeprowadzenia doświadczenia jest czyste, niezachmurzone niebo w każdej z miejscowości. Nam spełnienie tego warunku zajęło ponad miesiąc. Na koniec współpracujące szkoły dokonują dokładnie w tym samym czasie pomiaru długości cienia gnomu.
Doświadczenie zostało jednocześnie przeprowadzone 24 maja 2007 r. w dwóch punktach na Ziemi, w:
· Sopocie – Zespół Szkół Handlowych
(λ=18,567ºE, j=54,45ºN) – opiekun: niżej podpisany,
· Chorzowie – Zespół Szkół Gastronomiczno-Usługowych
(λ=18,944ºE, j=50,20ºN) – opiekun Pani Danuta Latos,
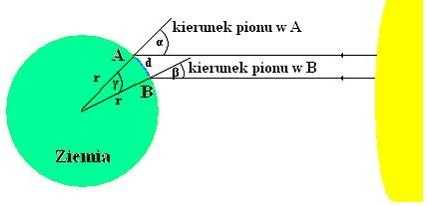
w dwóch seriach, czyli o godzinie 12.40 i 12.45 przez trzy grupy uczniowskie w każdej ze szkół (kontakt pomiędzy szkołami odbywał się przy wykorzystaniu telefonów komórkowych). Zadaniem uczniów było zmierzenie długości cienia gnomonu. A następnie obliczenie kątów padania promieni słonecznych (α, β). Ponieważ w obu miejscowościach kąt między kierunkiem pionu a kierunkiem na Słońce jest inny to otrzymane przez uczniów kąty padania promieni słonecznych są różne. Różnica tych kątów jest równa kątowi γ występującego oczywiście również w środku Ziemi, gdzie tworzą go obydwa piony (gnomony). Zatem można napisać proporcję
gdzie r – promień Ziemi, d – odległość południkowa między miejscami obserwacji.
Z analizy otrzymanych wyników widać, że błąd pomiaru naszych uczniów jest mniejszy od błędu Eratostenesa (ok. 5%). Co może wynikać z większej „zgodności południkowej” naszych miast i na pewno dokładniejszych pomiarów.
 |  |
Doświadczenie zostało jednocześnie przeprowadzone 24 maja 2007 r. w dwóch punktach na Ziemi, w:
· Sopocie – Zespół Szkół Handlowych
(λ=18,567ºE, j=54,45ºN) – opiekun: niżej podpisany,
· Chorzowie – Zespół Szkół Gastronomiczno-Usługowych
(λ=18,944ºE, j=50,20ºN) – opiekun Pani Danuta Latos,
w dwóch seriach, czyli o godzinie 12.40 i 12.45 przez trzy grupy uczniowskie w każdej ze szkół (kontakt pomiędzy szkołami odbywał się przy wykorzystaniu telefonów komórkowych). Zadaniem uczniów było zmierzenie długości cienia gnomonu. A następnie obliczenie kątów padania promieni słonecznych (α, β). Ponieważ w obu miejscowościach kąt między kierunkiem pionu a kierunkiem na Słońce jest inny to otrzymane przez uczniów kąty padania promieni słonecznych są różne. Różnica tych kątów jest równa kątowi γ występującego oczywiście również w środku Ziemi, gdzie tworzą go obydwa piony (gnomony). Zatem można napisać proporcję
| |
gdzie r – promień Ziemi, d – odległość południkowa między miejscami obserwacji.
Otrzymane wyniki
Przeprowadzone pomiary przez uczniów umożliwiły oszacowanie promienia (obwodu) Ziemi. Obliczenia przeprowadzone były dla średniej odległości Sopot-Chorzów d równej 470,17 km. Otrzymane wyniki przedstawia poniższa tabela.
| Godzina | Sopot | Chorzów | γ = <α>- <β> [º] | r [km] | Obwód Ziemi [km] | Błąd względny δ |
| <α> [º] | <β> [º] | |||||
| 12:40 | 33,91 | 29,54 | 4,37 | 6164,47 | 38732 | 2,92% |
| 12:45 | 33,77 | 29,4 | 4,37 | 6164,47 | 38732 | 2,92% |
Z analizy otrzymanych wyników widać, że błąd pomiaru naszych uczniów jest mniejszy od błędu Eratostenesa (ok. 5%). Co może wynikać z większej „zgodności południkowej” naszych miast i na pewno dokładniejszych pomiarów.
Wnioski
Z naszych obserwacji wynika, że gnomony krótkie wraz z wypoziomowaną tarczą powinny umożliwić otrzymanie dokładniejszych wyniki. A zastosowanie łączności internetowej wraz z kamerkami internetowymi pomiędzy szkołami dodatkowo uatrakcyjniłoby same doświadczenie. Także wykorzystanie systemu GPS do dokładnego wyznaczenia miejsce obserwacji przyczyniłoby się do podniesienia wartości dydaktycznej samego doświadczenia.
Dane dotyczące Ziemi
promień równikowy - 6378 km
promień biegunowy - 6357 km
obwód równika - 40076 km
długość południka - 20004 km
promień biegunowy - 6357 km
obwód równika - 40076 km
długość południka - 20004 km


 Instrukcja do ćwiczenia (pdf)
Instrukcja do ćwiczenia (pdf)